CIRCLES - Class IX, Ncert Cbse Mathematics Textbook Exercise 10.3 Solutions

CBSE Class IX, NCERT Solutions of Mathematics Textbook

Chapter 10, Circles - Exercise 10.3 (Solution)

(Page 176)

Q 1: Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?

Solution:

Consider the following pair of circles.

The above circles do not intersect each other at any point. Therefore, they do not have any point in common.

  

The above circles touch each other at 1 point X only. Therefore, the circles have 1 point in common.

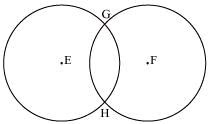
These circles intersect each other at two points G and H. Therefore, the circles have two points in common. It can be observed that there can be a maximum of 2 points in common. Consider the situation in which two congruent circles are superimposed on each other. This situation can be referred to as if we are drawing the circle two times.

Q 2: Suppose you are given a circle. Give a construction to find its centre.

Solution:

The below given steps will be followed to find the centre of the given circle.

Step1. Take the given circle.

Step2. Take any two different chords AB and CD of this circle and draw perpendicular bisectors of these chords.

Step3. Let these perpendicular bisectors meet at point O. Hence, O is the centre of the given circle.

Q 3: If two circles intersect at two points, then prove that their centers lie on the perpendicular bisector of the common chord.

Solution:

Consider two circles centered at point O and O’, intersecting each other at point A and B respectively.

Join AB. AB is the chord of the circle centered at O. Therefore, perpendicular bisector of AB will pass through O.

Again, AB is also the chord of the circle centered at O’. Therefore, perpendicular bisector of AB will also pass through O’.

Clearly, the centers of these circles lie on the perpendicular bisector of the common chord.